위상정렬(Topological Sorting) 알고리즘이란?
위상정렬 알고리즘이란 정렬 알고리즘의 일종으로, 선후관계가 존재하는 작업들을 순서에 맞게 나열할 때 사용하는 알고리즘이다. 즉, 사이클이 없는 방향 그래프(DAG, Directed Acyclic Graph)에서 모든 노드를 방향성을 위배하지 않도록 정렬한 순서를 의미한다.
예를 들어, 아래와 같이 총 3개의 과목이 있다고 해보자.
| 자료구조 | 알고리즘 | 데이터베이스 |
3개의 과목을 모두 듣기 위해 자료구조 → 알고리즘 → 데이터베이스 순서로 과목을 들어야한다면,
자료구조 → 데이터베이스 → 알고리즘과 같은 순서는 잘못된 학습 순서이다.
집입차수와 진출차수
- 진입차수(Indegree) : 특정 노드로 들어오는 간선의 수
- 진출차수(Outdegree) : 특정 노드에서 다른 노드로 나가는 간선의 수

위상정렬 알고리즘 동작 과정
위상정렬은 일반적으로 큐(Queue)를 이용해 구현한다.
동작 과정은 다음과 같다.
- 진입차수가 0인 모든 노드를 큐에 넣는다.
- 큐가 빌 때까지 반복한다.
- 큐에서 노드를 하나 꺼낸다.
- 꺼낸 노드에서 이어지는 모든 간선을 제거한다.
- 그로 인해 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
- 큐에서 꺼낸 노드의 순서가 위상정렬 결과가 된다.
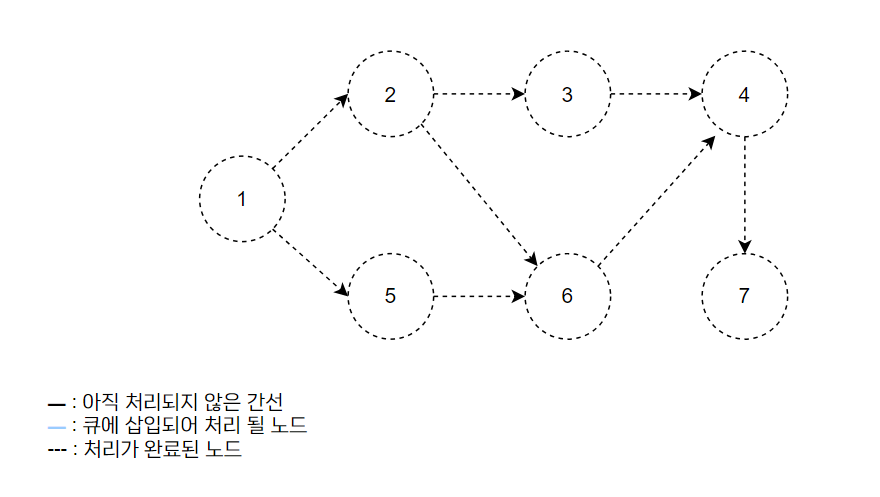
아래 그림을 통해 동작 과정을 이해해 보자.
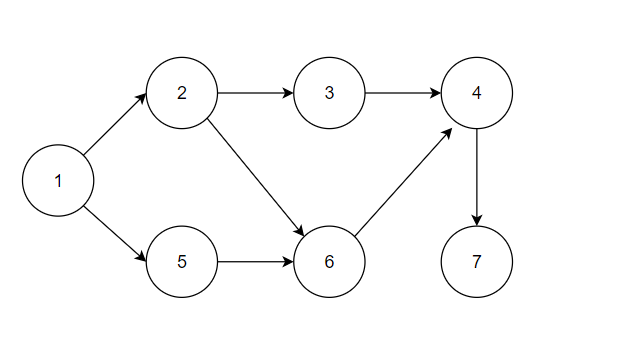
위 그림은 위상정렬을 수행할 그래프이다.
이때, 위상정렬을 수행할 수 있는 그래프는 사이클이 없는 방향성 비순환 그래프여야 한다.(일방향성)
[ 과정 0 ]
- 진입차수가 0인 노드를 모두 큐에 삽입한다.
- 현재 1번 노드의 진입차수만 0이므로 큐에 1번 노드만 삽입하게 된다.

[ 과정 1 ]
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 1 | 1 | 2 | 1 | 2 | 1 |
| 큐 | 노드 1 |
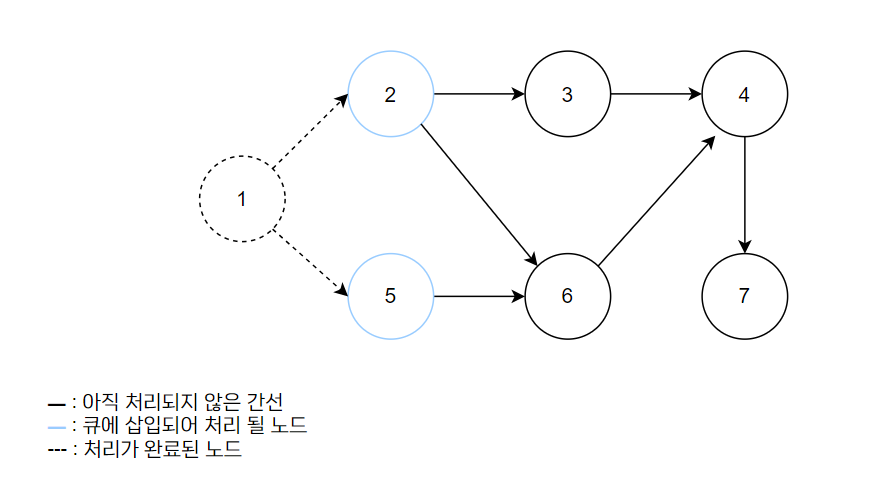
- 큐에 있는 1번 노드를 꺼낸다.
- 그 후, 1번 노드와 연결되어 있는 간선들을 제거한다.
- 2번 노드와 5번 노드의 진입차수는 0이 되고, 진입차수가 0인 2번 노드와 5번 노드를 큐에 삽입한다.
[ 과정 2 ]
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 1 | 2 | 0 | 2 | 1 |
| 큐 | 노드 2, 노드 5 |
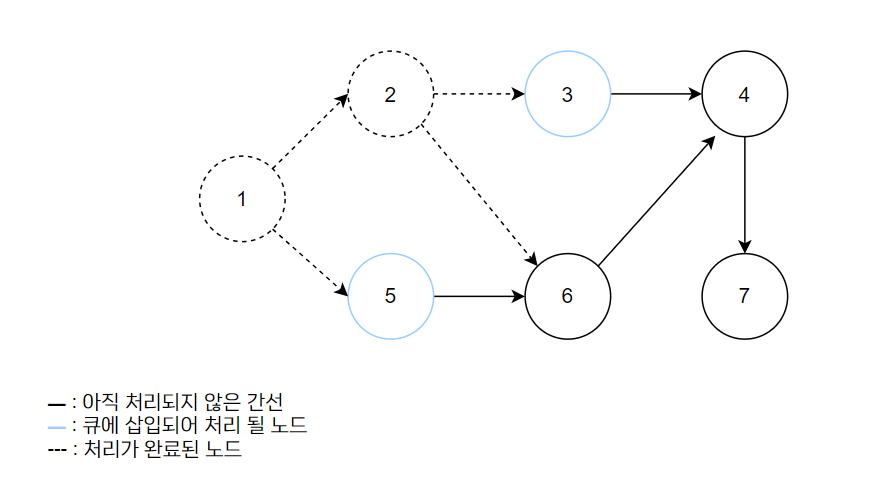
- 큐에 있는 2번 노드를 꺼낸다.
- 2번 노드와 연결되어 있는 간선들을 제거한다.
- 3번 노드의 진입차수가 0이 되고, 진입차수가 0인 3번 노드를 큐에 삽입한다.
[ 과정 3 ]
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 2 | 0 | 1 | 1 |
| 큐 | 노드 5, 노드 3 |
- 큐에 있는 5번 노드를 꺼낸다.
- 5번 노드와 연결되어 있는 간선들을 제거한다.
- 6번 노드의 진입차수가 0이 되고, 진입차수가 0인 6번 노드를 큐에 삽입한다.

[ 과정 4 ]
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 2 | 0 | 0 | 1 |
| 큐 | 노드 3, 노드 6 |
- 큐에 있는 3번 노드를 꺼낸다.
- 3번 노드와 연결되어 있는 간선들을 제거한다.
- 새롭게 진입차수가 0이 되는 노드가 없으므로 넘어간다.

[ 과정 5 ]
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 큐 | 노드 6 |
- 큐에 있는 6번 노드를 꺼낸다.
- 6번 노드와 연결되어 있는 간선들을 제거한다.
- 4번 노드의 진입차수가 0이 되고, 진입차수가 0인 4번 노드를 큐에 삽입한다.

[ 그 외 과정 ]
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 큐 | 노드 4 |
- 위와 동일한 로직으로 큐에 있는 노드를 꺼내고, 꺼낸 노드와 연결되어 있는 간선들을 제거한다.
- 새롭게 진입차수가 0이 되는 노드를 큐에 삽입한다.
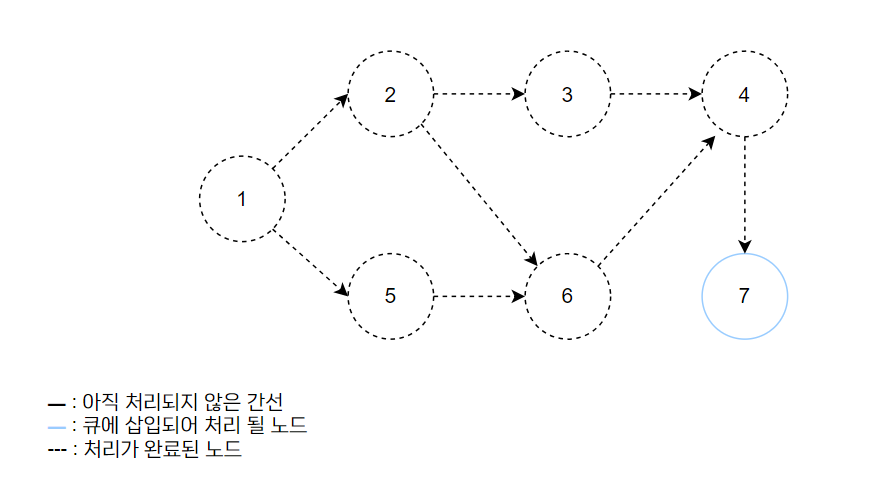
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 큐 | 노드 7 |
| 노드 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 진입차수 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 큐 |
[ 결과 ]
1 → 2 → 5 → 3 → 6 → 4 → 7
📍 위상 정렬은 여러 개의 답이 존재할 수 있다. 따라서 1 → 5 → 2 → 3 → 6 → 4 → 7도 하나의 답이 될 수 있다.
위상정렬 알고리즘 특징
- 위상정렬은 사이클이 없는 방향 그래프(DAG)에서만 수행할 수 있다.
- 위상정렬 결과는 여러 개가 존재할 수 있다.
- 특히, 특정 시점에 진입차수가 0인 노드가 여러 개일 경우
- 모든 노드를 방문하기 전에 큐가 비면 사이클이 존재함을 의미한다.
- 사이클에 포함된 노드는 진입차수가 0이 될 수 없기 때문이다.
- 일반적으로 큐(BFS 방식)를 사용하지만, 스택을 이용한 DFS 방식으로도 구현할 수 있다.
Java 구현 예시
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class sort {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 노드의 개수
int m = Integer.parseInt(st.nextToken()); // 간선의 개수
// 그래프 인접 리스트
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}
int[] indegree = new int[n+1]; // 각 노드의 진입차수 저장 배열
// 간선 입력
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
graph.get(from).add(to);
indegree[to]++; // 진입차수 증가
}
// 큐를 이용한 위상정렬
Queue<Integer> que = new LinkedList<>();
// 초기에 진입차수가 0인 노드들을 큐에 삽입
for (int i = 1; i <= n; i++) {
if (indegree[i] == 0) que.offer(i);
}
// 큐가 빌 때까지 반복
while (!que.isEmpty()) {
int node = que.poll();
// 큐에서 꺼낸 순서가 위상정렬 결과
sb.append(node).append(" ");
// 해당 노드와 연결된 모든 간선 제거
for (int next : graph.get(node)) {
indegree[next]--; // 진입차수 감소
// 새롭게 진입차수가 0이 된 노드를 큐에 삽입
if (indegree[next] == 0) {
que.offer(next);
}
}
}
System.out.println(sb.toString());
}
}
/* sample input
7 8
1 2
1 5
2 3
2 6
3 4
4 7
5 6
6 4
*/
📃 reference
'Algorithm' 카테고리의 다른 글
| 투 포인터(Two pointer)와 슬라이딩 윈도우(Sliding Window) (0) | 2024.07.27 |
|---|---|
| [자료구조] Deque(덱/데크) (2) | 2024.03.21 |
| [알고리즘] 슬라이딩 윈도우(Sliding window) (1) | 2023.12.04 |
| [알고리즘] 분할정복(Divide and Conquer) (0) | 2023.11.24 |
| [알고리즘] 다익스트라(Dijkstra) (0) | 2023.11.13 |

